Умножение скобок – это одна из основных операций в математике, которая позволяет получить результат умножения двух или более скобок. Для этого необходимо применить правило раскрытия скобок, при котором каждый элемент первой скобки умножается на каждый элемент второй скобки, а затем все полученные произведения складываются.
В следующих разделах статьи мы рассмотрим различные примеры умножения скобок, включая умножение многочленов, умножение скобок с переменными и умножение комплексных чисел. Вы узнаете основные правила и законы, которые помогут вам успешно выполнять эти операции и решать сложные математические задачи.
Основы умножения скобок
Умножение скобок — это математическая операция, которая позволяет перемножить выражения, заключенные в скобки. В результате умножения скобок получается новое выражение, которое может быть упрощено или раскрыто в дальнейшем.
Правило умножения скобок
Для умножения скобок необходимо каждый член первой скобки умножить на каждый член второй скобки. Ответом будет сумма произведений всех возможных комбинаций членов скобок.
Раскрытие скобок. 6 класс.
Например, у нас есть скобки (a + b) и (c + d). Для умножения этих скобок, необходимо умножить каждый член первой скобки (a и b) на каждый член второй скобки (c и d). Таким образом, получим:
| c | d | |
|---|---|---|
| a | a * c | a * d |
| b | b * c | b * d |
В итоге, результат умножения скобок (a + b) и (c + d) будет равен сумме всех полученных произведений: (a * c) + (a * d) + (b * c) + (b * d).
Примеры умножения скобок
Рассмотрим несколько примеров умножения скобок:
- Умножение скобок (2x + 3) и (4x — 5):
- 2x * 4x = 8x^2
- 2x * (-5) = -10x
- 3 * 4x = 12x
- 3 * (-5) = -15
- Умножение скобок (a + b) и (c — d):
- a * c = ac
- a * (-d) = -ad
- b * c = bc
- b * (-d) = -bd
Результат умножения скобок будет равен: 8x^2 — 10x + 12x — 15 = 8x^2 + 2x — 15.
Результат умножения скобок будет равен: ac — ad + bc — bd.
Важно помнить, что при умножении скобок порядок членов может меняться, но результат останется тем же.
Зачем умножать скобку на скобку?
Умножение скобки на скобку – это одна из важных операций в алгебре. Эта операция используется для раскрытия скобок и упрощения выражений. В результате умножения скобка на скобку мы получаем новое выражение, которое может быть проанализировано и дальше упрощено или решено.
Умножение скобки на скобку имеет свои правила, которые следует соблюдать при выполнении этой операции. Основное правило заключается в том, что каждый элемент первой скобки должен быть умножен на каждый элемент второй скобки. Таким образом, каждый элемент первой скобки будет умножен на каждый элемент второй скобки, а затем результаты сложатся.
Пример:
Рассмотрим простой пример: (a + b) * (c + d). Чтобы умножить эти скобки, умножим каждый элемент первой скобки на каждый элемент второй скобки:
- a * c
- a * d
- b * c
- b * d
Затем сложим полученные результаты:
(a + b) * (c + d) = a * c + a * d + b * c + b * d
Таким образом, мы раскрыли скобки и упростили выражение.
Умножение скобки на скобку часто используется в алгебре для упрощения сложных выражений, факторизации полиномов и решения уравнений. Понимание этой операции позволяет нам легче анализировать и решать математические задачи.
Правило умножения скобок
При умножении скобок нужно умножить каждый элемент первой скобки на каждый элемент второй скобки и сложить полученные произведения.
Например, если у нас есть скобки (a + b) и (c + d), то результат умножения будет:
- a * c
- a * d
- b * c
- b * d
Полученные произведения можно затем сложить для получения окончательного результата.
Также можно представить правило умножения скобок с помощью таблицы:
| c | d | |
|---|---|---|
| a | a * c | a * d |
| b | b * c | b * d |
Это правило умножения скобок может быть использовано для упрощения и вычисления сложных математических выражений. Например, если у нас есть выражение (2x + 3)(4x — 5), то мы можем использовать правило умножения скобок, чтобы умножить каждый элемент первой скобки на каждый элемент второй скобки и сложить полученные произведения. Это поможет нам получить результат этого выражения.
Примеры умножения скобок
Умножение скобок является одной из основных операций в алгебре. Применяется оно в различных математических и физических задачах, а также в программировании. Правила умножения скобок позволяют нам раскрыть скобки и упростить выражение.
Рассмотрим несколько примеров умножения скобок:
Пример 1:
Умножение двух одинаковых скобок:
(a + b)(a + b) = a2 + 2ab + b2
В данном примере мы раскрыли скобки и получили квадрат суммы двух переменных a и b.
Пример 2:
Умножение скобок с разными знаками:
(a + b)(a — b) = a2 — ab + ab — b2 = a2 — b2
В этом примере мы используем формулу разности квадратов, которая позволяет нам упростить выражение и получить разность квадратов двух переменных a и b.
Пример 3:
Умножение скобок с несколькими переменными:
(a + b + c)(x + y) = ax + ay + bx + by + cx + cy
В данном примере мы раскрываем скобки и получаем сумму произведений всех переменных. Здесь важно учесть, что каждая переменная из первой скобки умножается на каждую переменную из второй скобки.
Пример 4:
Умножение скобок с числами и переменными:
(2a + 3b)(4a — 5b) = 2a * 4a + 2a * (-5b) + 3b * 4a + 3b * (-5b) = 8a2 — 10ab + 12ab — 15b2 = 8a2 + 2ab — 15b2
В этом примере мы применяем правило умножения каждого члена первой скобки на каждый член второй скобки. Затем мы суммируем и упрощаем полученные произведения.
Это лишь некоторые примеры умножения скобок. В алгебре существуют и другие правила, которые позволяют упрощать выражения с умножением скобок. Важно помнить, что правильное применение этих правил позволяет нам упростить выражение и найти его значениe.
Как умножить скобку на число?
Умножение скобки на число — это математическая операция, которая позволяет умножить каждый элемент внутри скобки на заданное число. Для выполнения этой операции следует умножить число на каждый элемент внутри скобки, используя правило распределительного закона.
Чтобы умножить скобку на число, следуйте этим шагам:
- Распределите число на каждый элемент внутри скобки, используя закон распределения. Для этого умножьте число на каждый элемент внутри скобки.
- Запишите результаты умножения внутри скобки.
Например, если у вас есть скобка (3 + 4) и вы хотите умножить ее на число 2, следуйте этим шагам:
- Умножьте число 2 на каждый элемент внутри скобки: 2 * 3 = 6 и 2 * 4 = 8.
- Запишите результаты умножения внутри скобки: (6 + 8).
Таким образом, результат умножения скобки (3 + 4) на число 2 будет равен (6 + 8) = 14.
Этот метод работает не только с простыми выражениями, но и с более сложными. Например, если у вас есть скобка (2x + 3y) и вы хотите умножить ее на число 4, следуйте тем же шагам:
- Умножьте число 4 на каждый элемент внутри скобки: 4 * 2x = 8x и 4 * 3y = 12y.
- Запишите результаты умножения внутри скобки: (8x + 12y).
Таким образом, результат умножения скобки (2x + 3y) на число 4 будет равен (8x + 12y).
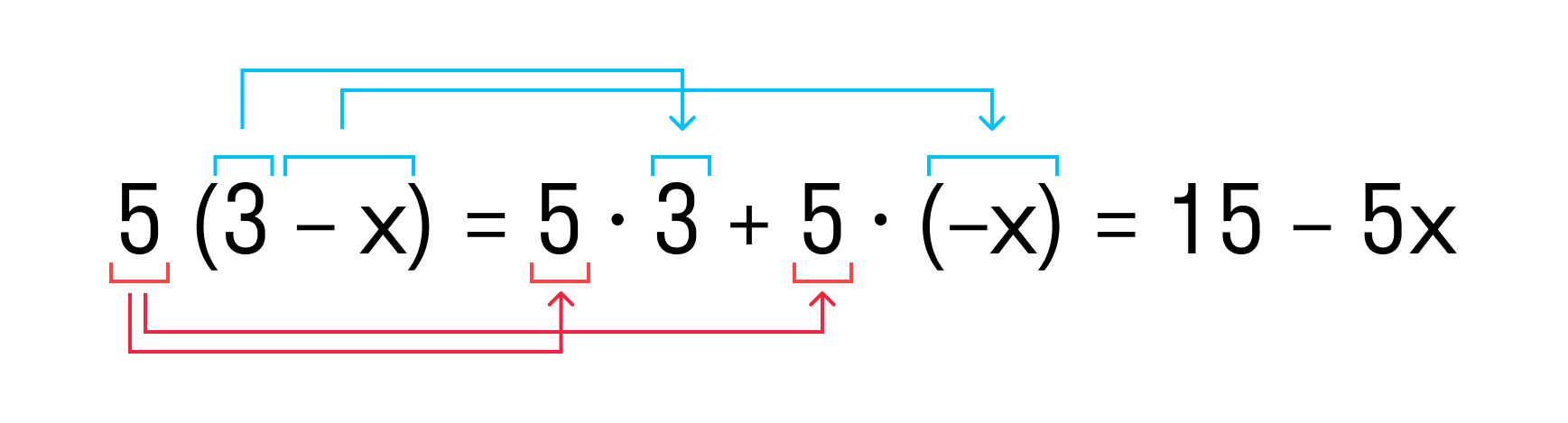
Как умножить скобку на переменную?
Умножение скобки на переменную является одним из фундаментальных математических операций, которые используются в алгебре и арифметике. Эта операция позволяет нам раскрыть скобку и умножить каждый элемент внутри скобки на переменную.
Для умножения скобки на переменную, нужно каждый элемент внутри скобки умножить на эту переменную. Например, если у нас есть скобка (a + b) и переменная x, то результат умножения будет таким:
x * (a + b) = x * a + x * b
В данном примере, мы раскрыли скобку и умножили каждый элемент внутри скобки на переменную x. Таким образом, получили два слагаемых — x * a и x * b.
Если скобка содержит несколько элементов, то умножение будет происходить для каждого элемента внутри скобки. Например, если у нас есть скобка (a + b + c) и переменная x, то результат умножения будет таким:
x * (a + b + c) = x * a + x * b + x * c
В данном примере, мы раскрыли скобку и умножили каждый элемент внутри скобки на переменную x. Таким образом, получили три слагаемых — x * a, x * b и x * c.
Умножение скобки на переменную является основополагающим принципом в алгебре и математике в целом. Оно позволяет нам работать с переменными и скобками, раскрывая их и умножая каждый элемент на нужную переменную. Этот принцип широко используется в решении уравнений, выражений и других математических задачах.
Полезные советы при умножении скобок
Умножение скобок – одна из основных операций в алгебре. В этой статье я расскажу вам несколько полезных советов, которые помогут вам умножать скобки правильно и эффективно.
1. Запомните правило распределения
Одним из основных правил при умножении скобок является правило распределения. Суть его заключается в том, что нужно умножить каждый член одной скобки на каждый член другой скобки, а затем сложить полученные произведения. Например, при умножении скобок (а + b) и (c + d) получим: (a * c) + (a * d) + (b * c) + (b * d).
2. Используйте таблицу умножения
Если у вас возникают затруднения с умножением чисел в скобках, помните, что всегда можно воспользоваться таблицей умножения. Запомните таблицу умножения наиболее часто встречающихся чисел от 1 до 10, и вам будет гораздо проще выполнять умножение скобок.
3. Пользуйтесь свойствами алгебры
Алгебра имеет множество свойств, которые могут существенно упростить умножение скобок. Например, свойство коммутативности позволяет менять порядок множителей, а свойство ассоциативности – менять порядок скобок. Используйте эти свойства, чтобы сделать умножение скобок более простым и удобным.
4. Учитывайте знаки чисел
При умножении скобок не забывайте учитывать знаки чисел. Если в одной из скобок есть отрицательное число, нужно помнить, что его знак изменится при перемножении с положительным числом. Например, (-a) * b = -ab.
5. Проверяйте результат
Не забывайте проверять полученный результат после умножения скобок. Возможно, в процессе вычислений вы допустили ошибку или пропустили какой-то шаг. Проверка поможет вам обнаружить и исправить возможные ошибки и убедиться, что ответ верный.
Следуя этим полезным советам, вы сможете умножать скобки без проблем и достичь более точных и быстрых результатов. Практика и тренировка помогут вам освоить этот навык, а затем вы сможете применять его в решении более сложных математических задач.




