Уравнения – это одна из важных тем в математике, которые изучаются на протяжении нескольких лет обучения. Обычно ученики начинают знакомиться с уравнениями в 7-8 классе, когда уже имеют базовые знания алгебры и геометрии. В дальнейшем, в более старших классах, изучение уравнений становится более глубоким и сложным.
В следующих разделах статьи мы рассмотрим, какие типы уравнений изучаются в разных классах, какие методы решения применяются, а также познакомимся с практическими примерами и задачами, которые помогут лучше понять и применить изученные материалы. Также мы расскажем о важности уравнений в реальной жизни и примерах их применения в различных областях.
Основные понятия
В математике уравнение — это математическое выражение, в котором указывается равенство двух алгебраических или тригонометрических выражений. Уравнения могут содержать различные переменные и константы, а также арифметические операции, такие как сложение, вычитание, умножение и деление.
Основные понятия, связанные с уравнениями, включают:
Решение простых уравнений. Что значит решить уравнение? Как проверить решение уравнения?
Переменная и константа
Переменная — это символ или буква, которая представляет неизвестное значение в уравнении. Она может принимать различные значения, но в каждом конкретном случае ей присваивается определенное значение. Например, в уравнении «x + 5 = 10», переменная «x» представляет неизвестное значение, которое мы пытаемся найти.
Константа — это значение, которое остается неизменным в уравнении. Она может быть числом или другим символом, который не зависит от переменной. В уравнении «x + 5 = 10», константами являются числа 5 и 10.
Линейное уравнение
Линейное уравнение — это уравнение степени 1, в котором переменная входит только в первой степени. Оно имеет вид «ax + b = c», где «a», «b» и «c» — это константы, а «x» — переменная. Примером линейного уравнения является «2x + 3 = 7». Чтобы решить линейное уравнение, нужно найти значение переменной, удовлетворяющее равенству.
Квадратное уравнение
Квадратное уравнение — это уравнение степени 2, в котором переменная входит во второй степени. Оно имеет вид «ax^2 + bx + c = 0», где «a», «b» и «c» — это константы, а «x» — переменная. Примером квадратного уравнения является «x^2 + 5x + 6 = 0». Чтобы решить квадратное уравнение, нужно найти значения переменной, удовлетворяющие равенству.
Решение уравнения
Решение уравнения — это значение или набор значений переменной, которые удовлетворяют равенству в уравнении. Например, если в уравнении «2x + 3 = 7» найдено значение переменной «x = 2», то оно является решением данного уравнения.
В школьной программе уравнения изучаются в различных классах, начиная с элементарной школы. В начальной школе учатся простые уравнения, состоящие из одной переменной и выполняющиеся по принципу «одной операции — одно решение». В средней школе изучаются более сложные уравнения, такие как линейные и квадратные уравнения. В старших классах изучается решение систем уравнений и уравнений высших степеней.
Младшие классы
Младшие классы – это начальная ступень образования, которая предшествует средней и старшей школе. В младших классах дети получают основное образование и осваивают основные навыки и знания, необходимые для успешного обучения в будущем.
Организация обучения
В младших классах обучение организовано по предметно-тематическому принципу. Это означает, что каждый предмет изучается в отдельности, а знания и навыки постепенно увеличиваются и усложняются с каждым классом. Основные предметы, которые изучаются в младших классах, включают математику, русский язык, окружающий мир, литературу, иностранный язык, технологию, музыку и изобразительное искусство.
Уровень сложности
Уровень сложности уроков и заданий в младших классах соответствует возрастным возможностям детей. Учитель старается сделать уроки интересными и доступными для понимания, используя игровые и интерактивные методы обучения. Учебники и рабочие тетради, используемые в младших классах, разработаны с учетом возрастных особенностей детей и направлены на развитие их познавательных способностей.
Уравнения в младших классах
В младших классах изучение уравнений еще не проводится. Уравнения – это математические выражения, в которых неизвестная величина обозначается буквой и находится путем решения. Сложность уравнений возрастает с каждым классом, поэтому их изучение начинается только в средней или старшей школе. В младших классах дети изучают основы математики, такие как счет, арифметические операции, геометрию и изучение чисел и их свойств.
Таким образом, младшие классы – это первый шаг в образовании, где дети получают основные знания и навыки, необходимые для успешной учебы в дальнейшем. Важно, чтобы обучение в младших классах было интересным и понятным для детей, чтобы они могли развиваться и учиться с удовольствием.
Средние классы
Средние классы – это период обучения в школе, который следует за начальной школой и предшествует старшей школе. Обычно средние классы включают в себя 6-9 классы, хотя в некоторых странах или школьных системах этот период может варьироваться.
В средних классах учащиеся продолжают изучение основных учебных предметов, таких как математика, русский язык, иностранный язык, история, география, физика, химия и биология. Кроме того, в этом периоде вводятся новые предметы, например, алгебра и геометрия.
Уравнения в средних классах
Уравнения являются важной частью математического курса в средних классах. Обычно изучение уравнений начинается в 7-8 классе, хотя в некоторых школах они могут быть введены раньше или позже. Уравнения помогают учащимся развивать навыки аналитического мышления, логики и решения проблем.
В средних классах учащиеся изучают линейные уравнения с одной переменной, такие как 2x + 5 = 13. Они учатся находить неизвестную переменную, решая уравнение. Также вводятся понятия коэффициента, свободного члена и решения уравнения.
Уравнения представляют собой важный инструмент для решения различных задач и проблем в математике и других науках. Они также имеют практическое применение в реальной жизни, например, для решения задач финансового планирования или оценки производительности системы.
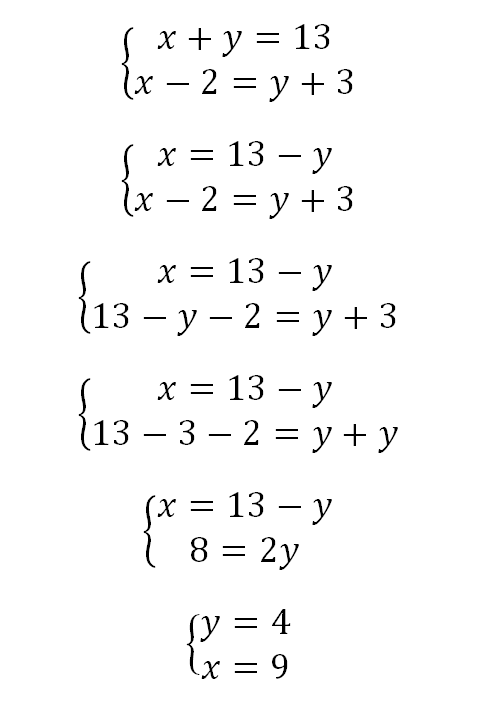
Старшие классы
Старшие классы включают в себя 10-11 классы, которые являются завершающим этапом среднего образования. В этих классах ученики готовятся к сдаче выпускных экзаменов и получению аттестата о среднем образовании.
Один из важных разделов программы старших классов – уравнения и системы уравнений. Уравнения – это математические задачи, которые требуют нахождения неизвестного значения. В школьной программе старших классов изучаются уравнения первой и второй степени, а также системы уравнений.
Уравнения первой степени
Уравнения первой степени имеют вид ax + b = 0, где a и b – известные числа, а x – неизвестное значение. Чтобы найти значение x, необходимо применить различные методы решения уравнений. Один из таких методов – метод подстановки, который заключается в последовательном подставлении различных значений x и проверке удовлетворения уравнению. Другим методом является метод баланса, при котором уравнение преобразуется таким образом, чтобы неизвестное значение оказалось в одной части уравнения.
Уравнения второй степени
Уравнения второй степени имеют вид ax^2 + bx + c = 0, где a, b и c – известные числа, а x – неизвестное значение. Решение уравнений второй степени осуществляется с использованием формулы дискриминанта и метода исключения корня. Формула дискриминанта позволяет определить, сколько корней имеет уравнение, а метод исключения корня позволяет найти значение x, исключая корень из уравнения.
Системы уравнений
Системы уравнений состоят из нескольких уравнений, которые имеют общее решение. В школьной программе старших классов изучаются системы уравнений с двумя и тремя переменными. Для решения систем уравнений используются методы подстановки, метод сложения и вычитания, а также метод графического решения.
Подготовка к ЕГЭ и ОГЭ
ЕГЭ (единый государственный экзамен) и ОГЭ (основное государственное экзамен) являются важными этапами в жизни каждого школьника. Он определяет не только их перспективы поступления в вуз, но и уровень знаний, полученных в течение всего периода обучения. Подготовка к экзаменам требует времени, усилий и правильного подхода.
Особенности ЕГЭ и ОГЭ
ЕГЭ и ОГЭ отличаются друг от друга по формату и уровню сложности. ОГЭ является первым экзаменом, который сдают ученики после 9 класса. Он проверяет знания по основным предметам и является своеобразной пробой перед ЕГЭ. ЕГЭ проводится после окончания 11 класса и включает в себя более глубокую проверку знаний по выбранным предметам.
ЕГЭ и ОГЭ состоят из разных блоков заданий, включающих в себя тестовые задания, задания с кратким ответом, задания с развернутым ответом и практические задания. Результаты экзаменов определяются баллами, которые затем используются для поступления в вузы или получения аттестата о среднем образовании.
Подготовка к ЕГЭ и ОГЭ
Подготовка к ЕГЭ и ОГЭ требует систематического подхода и правильного планирования времени. Важно начать подготовку заранее, чтобы иметь достаточно времени для повторения и углубленного изучения материала.
Существует множество способов подготовки к экзаменам, включая самостоятельное изучение учебников, посещение курсов подготовки, участие в онлайн-тренировках и решение типовых заданий. Каждый школьник должен выбрать тот метод, который ему больше всего подходит и помогает лучше усвоить материал.
Рекомендации по подготовке
Для эффективной подготовки к ЕГЭ и ОГЭ полезно придерживаться следующих рекомендаций:
- Составить план подготовки: разделить материал на блоки и распределить время на изучение каждого блока.
- Регулярно повторять материал: проводить периодические повторения, чтобы закрепить знания и улучшить понимание тем.
- Решать типовые задания: решать задания, аналогичные тем, которые могут встретиться на экзаменах, чтобы попрактиковаться и оценить свой уровень подготовки.
- Обращаться за помощью: при возникновении трудностей не стесняться обращаться за помощью к учителям или репетиторам, которые могут объяснить сложные темы и помочь разобраться с заданиями.
- Поддерживать здоровый образ жизни: важно уделять внимание физической активности, правильному питанию и достаточному количеству сна, чтобы быть в хорошей физической и психологической форме во время экзаменов.
Подготовка к ЕГЭ и ОГЭ требует времени и усилий, но с правильным подходом и настойчивостью каждый школьник может достичь успеха и получить хорошие результаты на экзаменах.




